import numpy as np
import matplotlib.pyplot as plt
# 生成一个更复杂的示例信号
N = 1024
t = np.arange(N)
signal = np.sin(2 * np.pi * 5 * t / N) + 0.5 * np.sin(2 * np.pi * 50 * t / N) + 0.3 * np.sin(2 * np.pi * 120 * t / N)
# 应用Hamming窗
hamming_window = np.hamming(N)
windowed_signal = signal * hamming_window
# 增加频谱分辨率(零填充)
zero_padded_signal = np.pad(signal, (0, 3*N))
zero_padded_windowed_signal = np.pad(windowed_signal, (0, 3*N))
# 进行FFT
fft_original = np.fft.fft(zero_padded_signal)
fft_windowed = np.fft.fft(zero_padded_windowed_signal)
# 放大频谱细节部分
zoom_factor = 100
# 频谱显示
fig, axs = plt.subplots(3, 2, figsize=(14, 15))
# 原始信号时域图
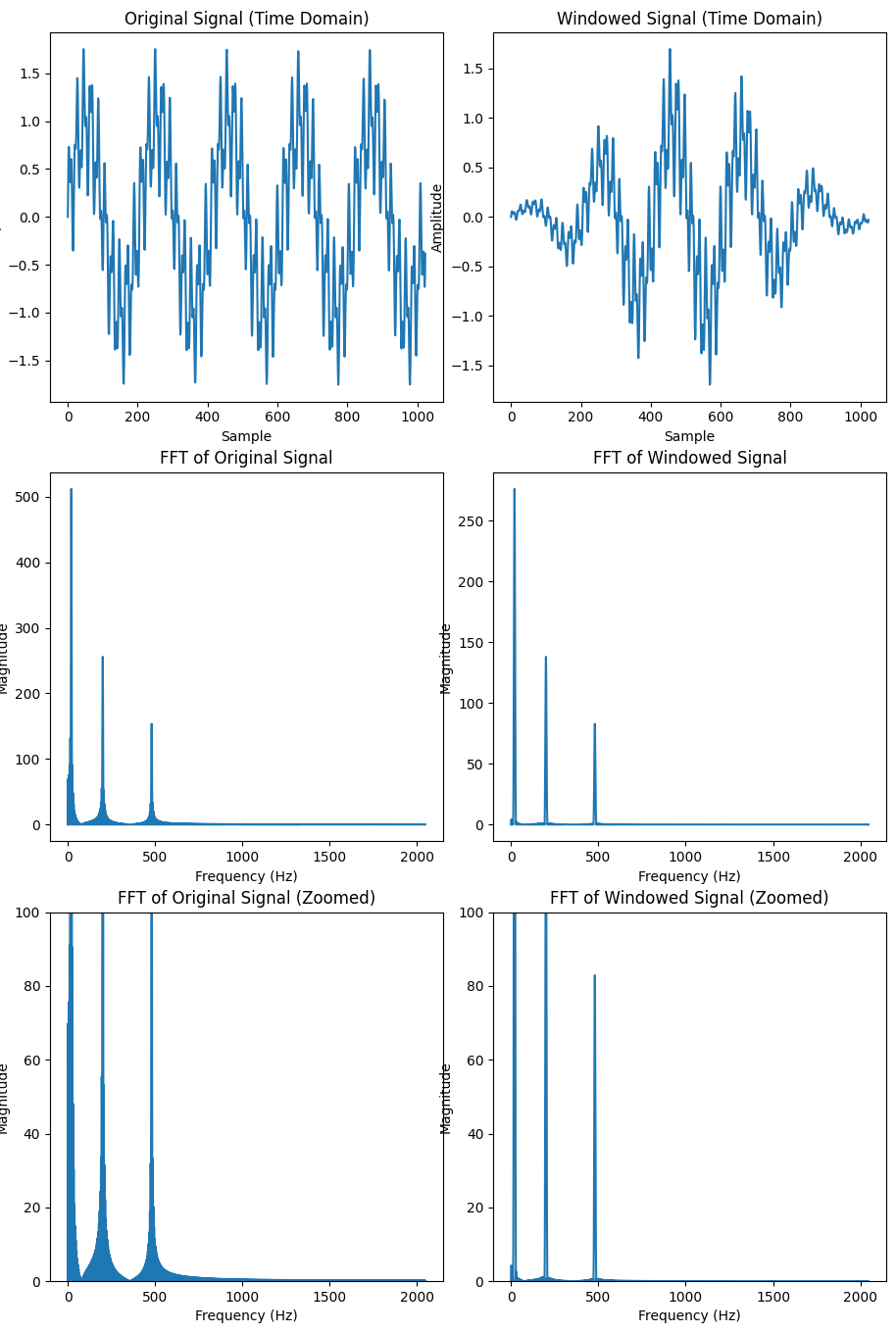
axs[0, 0].plot(signal)
axs[0, 0].set_title('Original Signal (Time Domain)')
axs[0, 0].set_xlabel('Sample')
axs[0, 0].set_ylabel('Amplitude')
# 加窗信号时域图
axs[0, 1].plot(windowed_signal)
axs[0, 1].set_title('Windowed Signal (Time Domain)')
axs[0, 1].set_xlabel('Sample')
axs[0, 1].set_ylabel('Amplitude')
# 原始信号频域图
axs[1, 0].plot(np.abs(fft_original)[:len(fft_original) // 2])
axs[1, 0].set_title('FFT of Original Signal')
axs[1, 0].set_xlabel('Frequency (Hz)')
axs[1, 0].set_ylabel('Magnitude')
# 加窗信号频域图
axs[1, 1].plot(np.abs(fft_windowed)[:len(fft_windowed) // 2])
axs[1, 1].set_title('FFT of Windowed Signal')
axs[1, 1].set_xlabel('Frequency (Hz)')
axs[1, 1].set_ylabel('Magnitude')
# 原始信号频域图(放大)
axs[2, 0].plot(np.abs(fft_original)[:len(fft_original) // 2])
axs[2, 0].set_ylim(0, zoom_factor)
axs[2, 0].set_title('FFT of Original Signal (Zoomed)')
axs[2, 0].set_xlabel('Frequency (Hz)')
axs[2, 0].set_ylabel('Magnitude')
# 加窗信号频域图(放大)
axs[2, 1].plot(np.abs(fft_windowed)[:len(fft_windowed) // 2])
axs[2, 1].set_ylim(0, zoom_factor)
axs[2, 1].set_title('FFT of Windowed Signal (Zoomed)')
axs[2, 1].set_xlabel('Frequency (Hz)')
axs[2, 1].set_ylabel('Magnitude')
plt.tight_layout()
plt.show()
